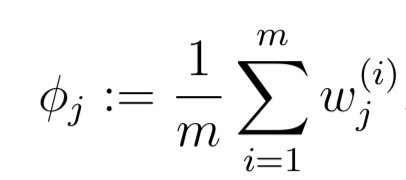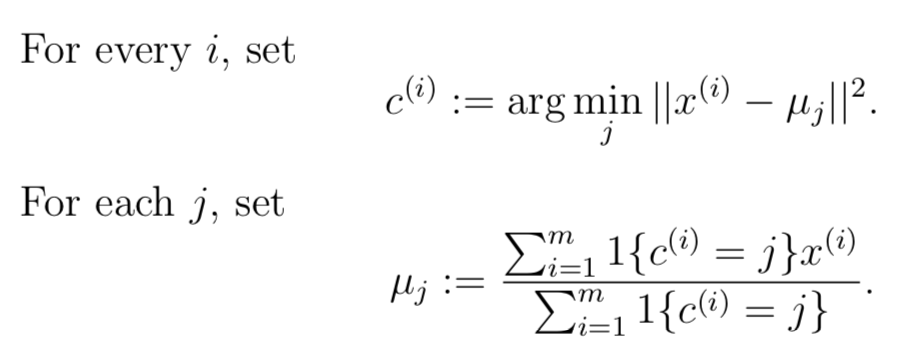Lecture 12 k-means, 混合高斯分布, EM算法
本节主要讨论非监督学习的集中算法
1. k-means clustering algorithm
k-means算法是一种无监督的聚类算法,给定一个训练结合{x(1), . . . , x(m)},并没有标签y的信息,k-means的目的是将数据分为若干簇(cluster)。k-means算法比较简单且容易理解,具体算法流程如下:
-
- 随机初始化每个cluster的中心 μ1, μ2, . . . , μk ∈ Rn
-
- 重复一下流程直到收敛:
-
其中k表示cluster的大小,μj代表cluster j的中心位置,c表示样本所属的cluster。内循环中主要包含两个步骤:(1)判定每个样本x(i)所属的cluster j,并将该样本指派给相应cluster (2)根据cluster包含的样本,重新计算中心位置μj。下图以2个cluster为例
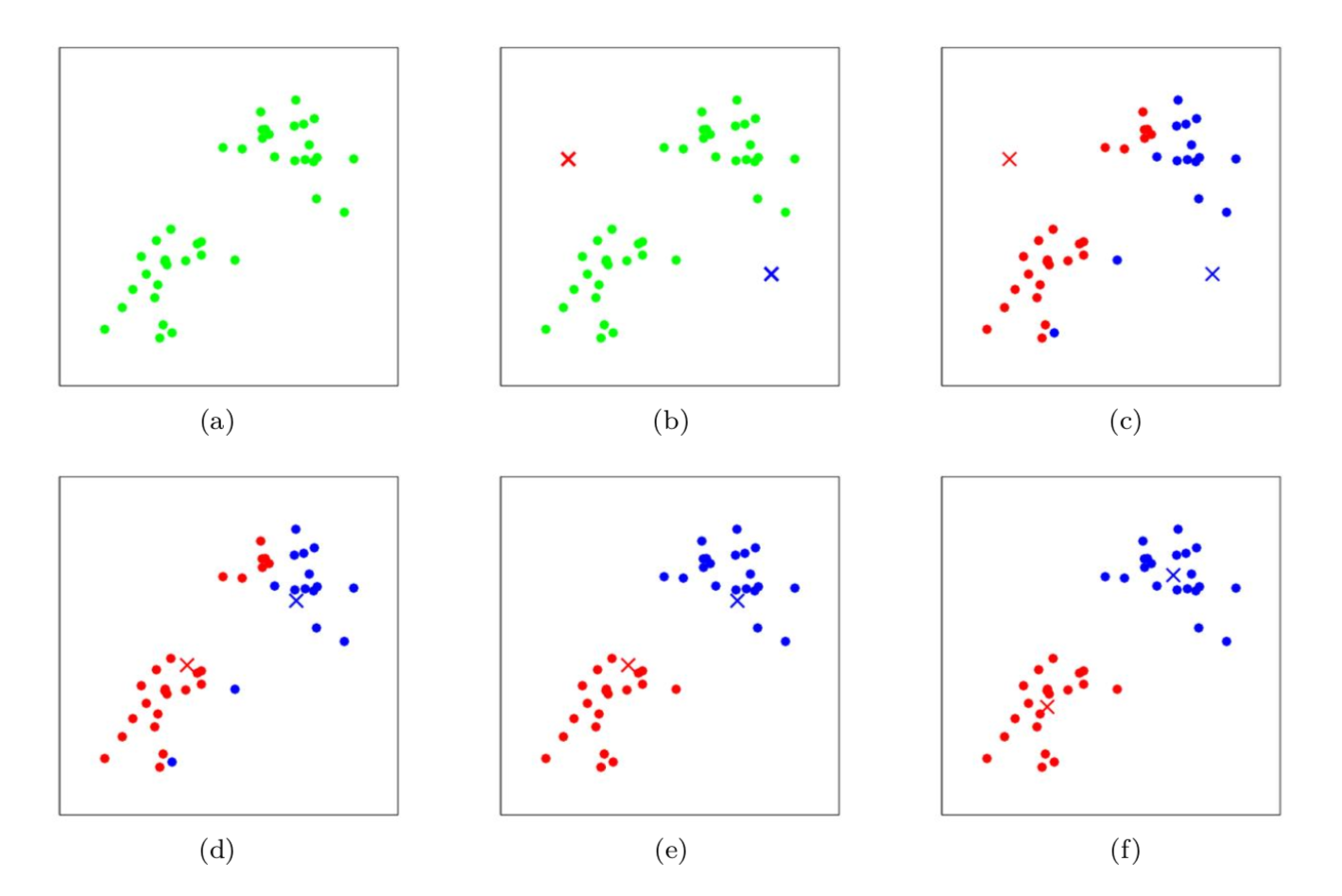
上图是迭代过程中,cluster的中心μ的变化过程:
- (a)原始数据集
- (b)随机初始化每个cluster的中心 μ1, μ2
- (c-f)迭代过程:2 iterations
-
- (c)根据与中心的距离,判定每个样本x(i)所属的cluster j,并将该样本指派给相应cluster,图中用颜色区分
-
- (d)根据cluster包含的样本,重新计算中心位置μj,因此中心μ1和μ2发生变化。
-
- (e)根据新的中心μ1和μ2,将样本重新指派给最近的cluster
-
- (f)根据重新指派后的样本归属,重新计算cluster的中心
那么,k-means就一定会收敛么?答案是肯定的,首先我们定义失真函数(distortion function):
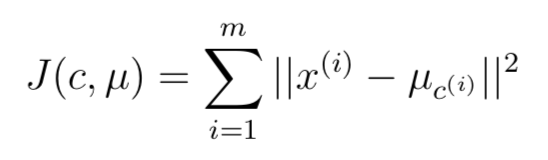
因此,函数J代表了样本与cluster中心的平方距离,那么k-means也就可以看作是针对J的坐标下降。k-means的内部循环中做的就是固定μ 之后最小化函数失真函数J;之后固定c 最小化J。因此J一定是单调下降的,也就一定会收敛。
失真函数J是非凸(non-convex)函数,所以对于J的坐标下降不一定会收敛到全剧最优解,因此又可能会得到局部最优解。这种情况下,通常的做法是利用不同的初始值,训练多次,最后选择失真函数J最小的一种聚类方式。
2. 混合高斯分布 Mixtures of Gaussians
给定一组训练数据{x(1), . . . , x(m)},由于非监督因此没有标签数据。首先看课中提高的一个例子,假设只有两类样本用叉和圆圈表示,下图给出了特征x的概率密度情况:
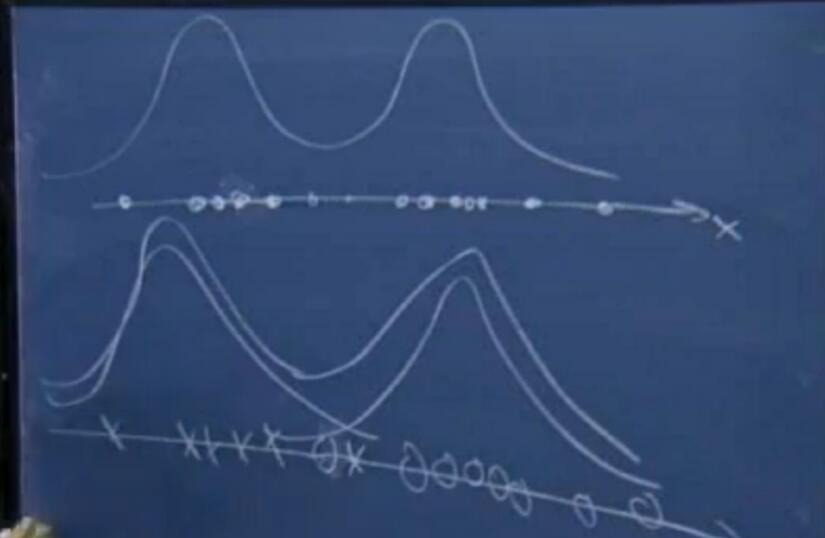
每个特征的真实分布,是由两个高斯分布一起产生的,只不过影响大小不同。
这里我们引出一个隐(latent)变量z服从多项式分布z(i) ∼ Multinomial(φ),其中φj表示p(z(i) = j),因此 φj ≥ 0 且 φj的和为1。同时假设x(i)|z(i) = j ∼ N(μj,Σj)也就是服从高斯分布。假设z有k个取值,那么就可以给出联合概率分布:
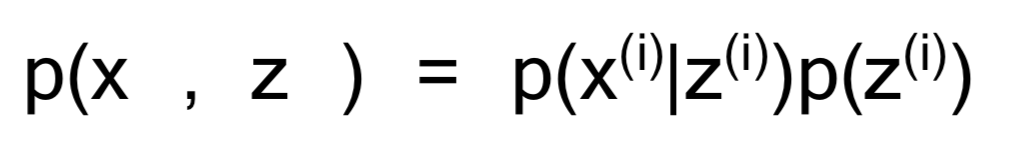
可以这样理解:首先从k个高斯分布中随机产生一个z(i),之后生成样本x(i)。 因此,模型针对参数φ, μ 和 Σ 的似然函数如下:
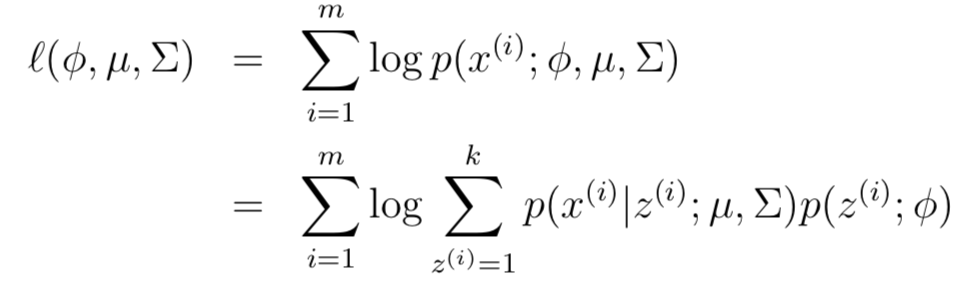
但是利用常规的求导数=0,并不能解出其中的参数。但是,如果z已知的话,那么上述似然函数就与之前讲过的高斯判别模型一模一样了,只不过y换成了z。下面是高斯判别模型的最终参数估计形式:
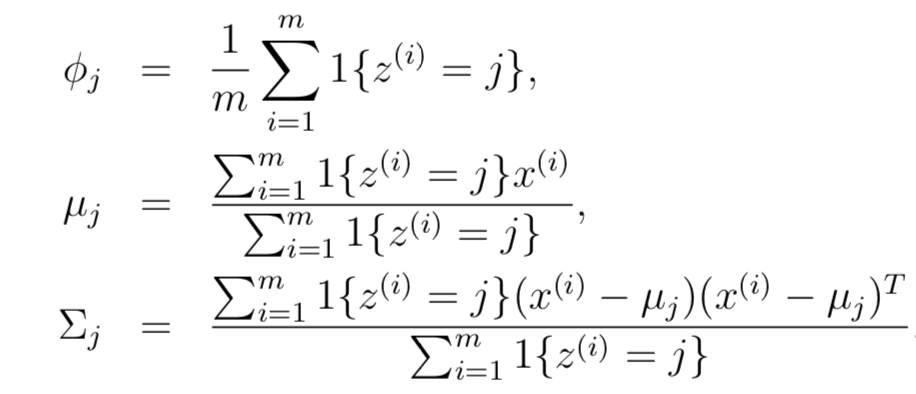
但是我们并不知道z的值,该怎么办呢? 答案是EM算法
3. EM算法
EM算法是一种迭代式算法,主要包含两个步骤:
- E-Step: “猜” z(i)的值
- M-Step: 根据z(i)的值,更新模型的参数
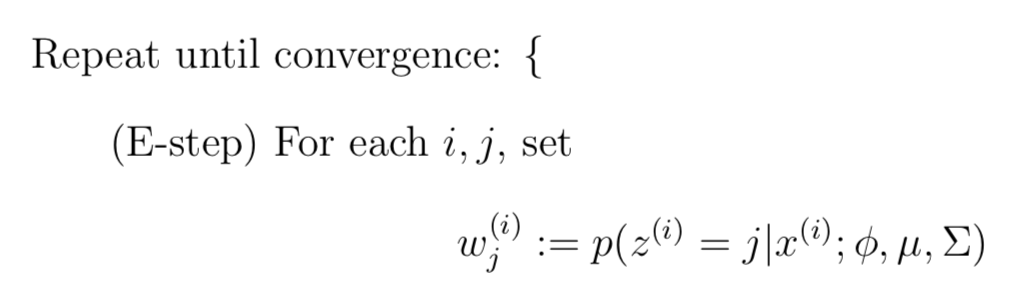

在E-Step,为了计算z(i)的后验概率,在给定当前模型参数的情况下,根据贝叶斯rule 可以得到:
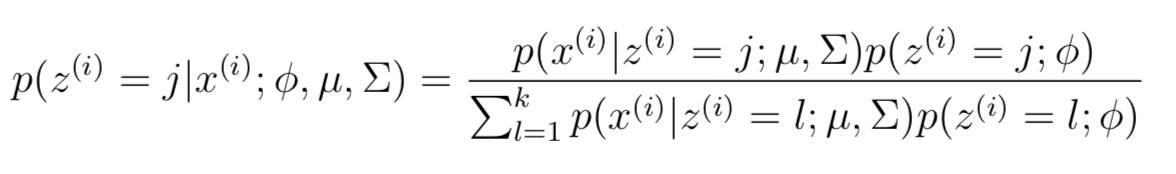
其中p(x(i)|z(i) = j;μ,Σ)根据高斯密度函数估计。w(i)表示对在(i)的一种软估计(soft guesses)。在M-Step知道了z(i)的值,就可以类似高斯判别分析的方法计算更新模型参数了,只不过其中的指示函数I{z(i) = j}变成了wj(i)。
与k-means对比,k-means是一种对c(i)的硬(hard)指派;而混合高斯是一种soft的指派,利用概率分布来计算wj(i)。与k-means类似,混合高斯分布也存在出现局部最优解的可能。
这里只是给出了EM算法的流程,但是并没有给出原因,例如为什么E-Step的“guess”是正确的?
3-1. EM算法原理
3-1-1. 杰森不等式Jensen’s inequality
对于数值函数f,如果所有的x,二阶导数f′′(x) ≥ 0,那么函数f就是凸(convex)函数。那么对于向量形式来说,就是如果还塞矩阵是半正定的H ≥ 0,那么f就是凸的。严格凸函数则 H > 0。
以上是基础的矩阵知识,下面给出杰森不等式:
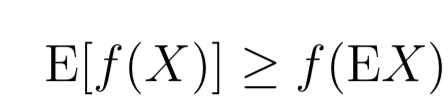
如果f是严格凸的,那么当且仅当X = E[X](X是常数),等号才成立E[f(X)] = f(EX)。下面直观理解Jensen不等式:
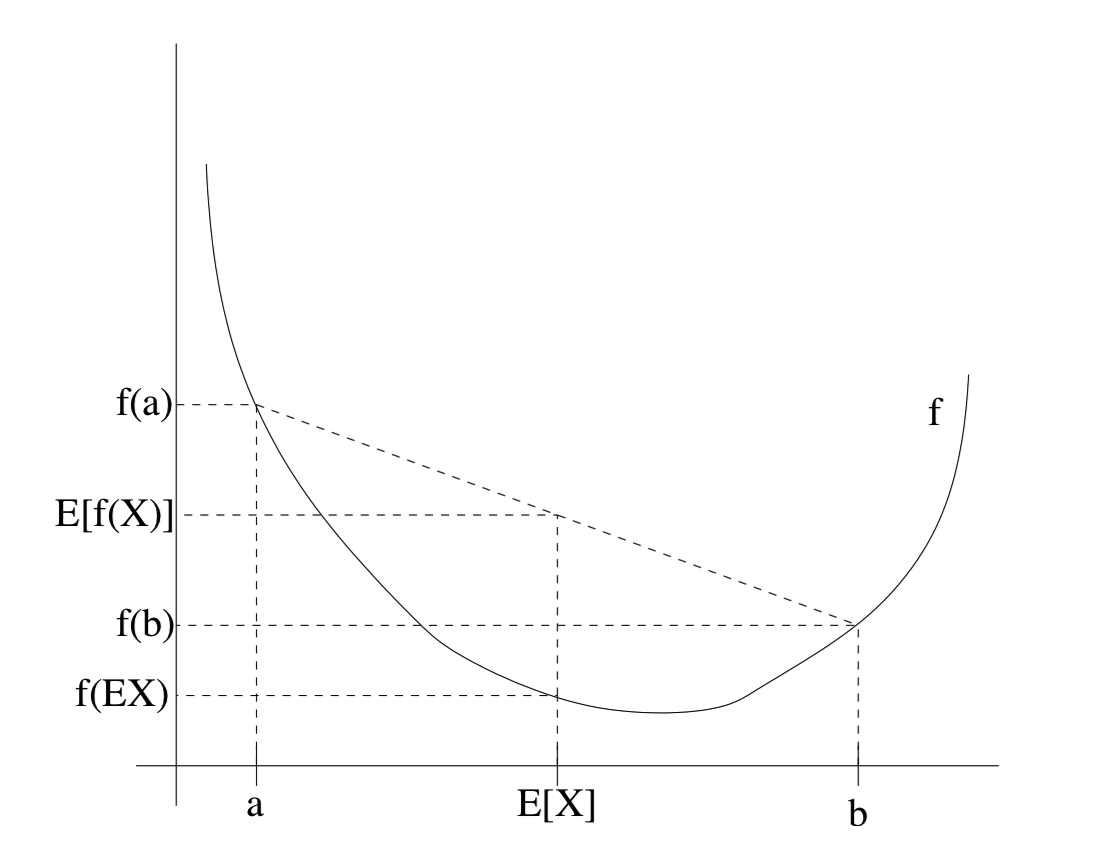
从图中可以直观看到这一点:两个点函数值的平均值>=两个点平均值对应的函数值。也就是凸函数中函数值的期望>=期望的函数值。
3-1-2. EM算法
假设存在一组包含m个样本训练集合{x(1), . . . , x(m)},引入一个latent变量之后,其似然函数为:
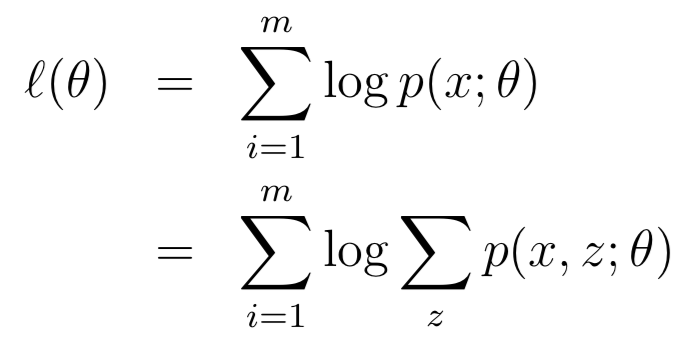
因为z是latent的,所以极大似然估计无法求解。在这种情况下,EM算法的思路是:无法确定l(θ) ,那么就(E-Step)构造l(θ) 的下界(lower-bound)函数,之后(M-Step)对下界(lower-bound)函数进行最优化。下面直观理解一下为什么采用下界函数:
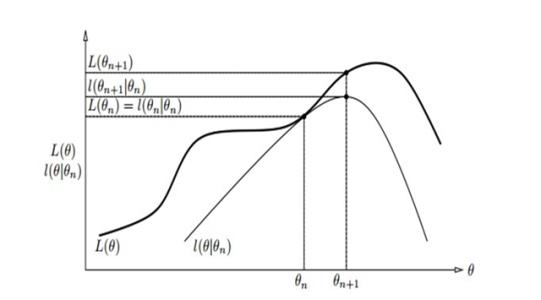
假设当前处于θn的位置,对于l(θ)无法优化,那么我们就找到l(θ)的一个下界函数,就是图中的l(θ|θn),并让两个函数在θn处重合相交。之后只要对下界函数求解最大值(θn+1处),那么对应的l(θ)也一定变大,即处于优化过程。
接下来从公式推导角度进行分析,另Qi表示z的概率分布,那么Sum[Qi(z)]=1 且 Qi(z)≥0,因此可以对似然函数l(θ)进行如下变换
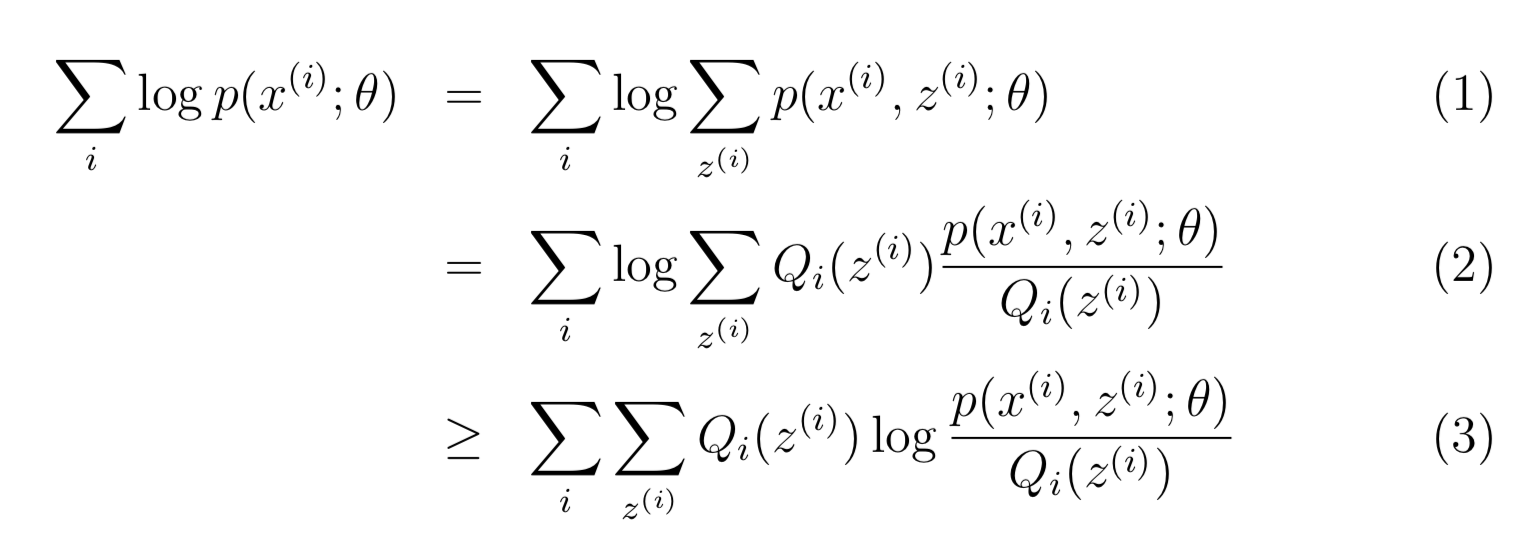
上面最后一步(3)就是采用了Jensen不等式,其中对应的f=log(x),因为f′′(x) = −1/x2 < 0 因此f是凹函数。而其中的
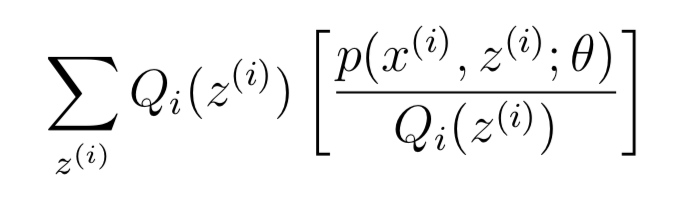
可以看作是[p(x(i), z(i); θ)/Qi(z(i))]的基于变量z(i)的(概率分布为Qi)期望。根据Jensen不等式:期望的函数值>=函数值的期望
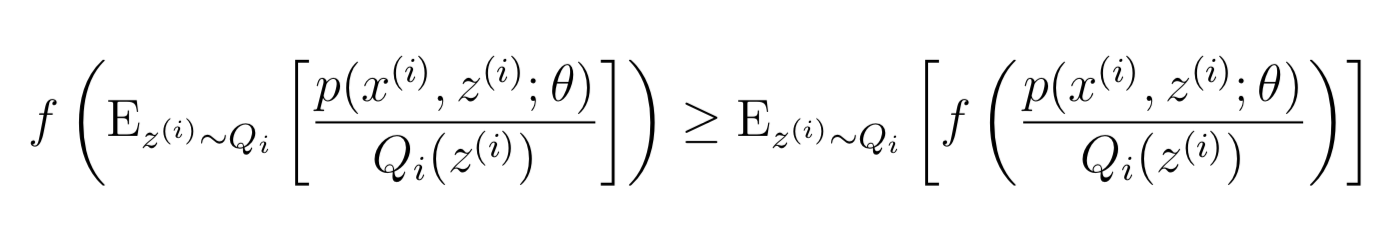
其中“z(i) ∼ Qi”表示期望是基于z(i)的,同时概率分布是Qi。根据这个Jensen不等式就可以从公式(2)推导出公式(3)。
因此,只要给定任意一个概率分布 Qi,就可以根据公式(3)得到l(θ)的下界。还有一个很重要的一点:我们要保证在θ处l(θ)与下界函数相交,也就是Jensen不等式的等号要成立。我们在上文讲到过,等号成立的条件是X = E[X] 也就是X是常数,任意常数都可以,因此可以另
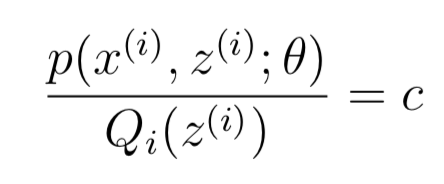
也就是说Q与p成正比:
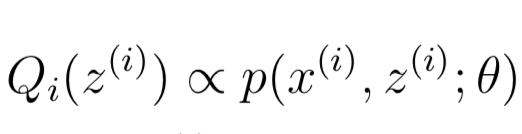
同时,因为Q是概率分布,因此Sum[Qi(z(i))] = 1, 从而可以推导出如下公式:
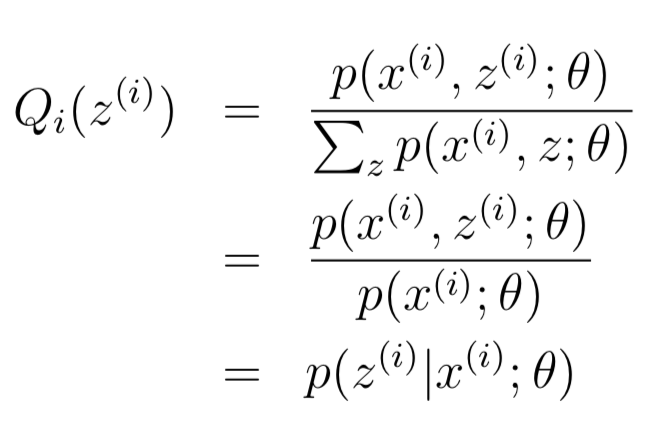
其实Q就是z(i)关于x(i)的后验分布。将Q带入公式(3)就可以得到l(θ)的下届lower-bound,之后对其进行maximize即可。由此可以得出EM算法的具体流程:
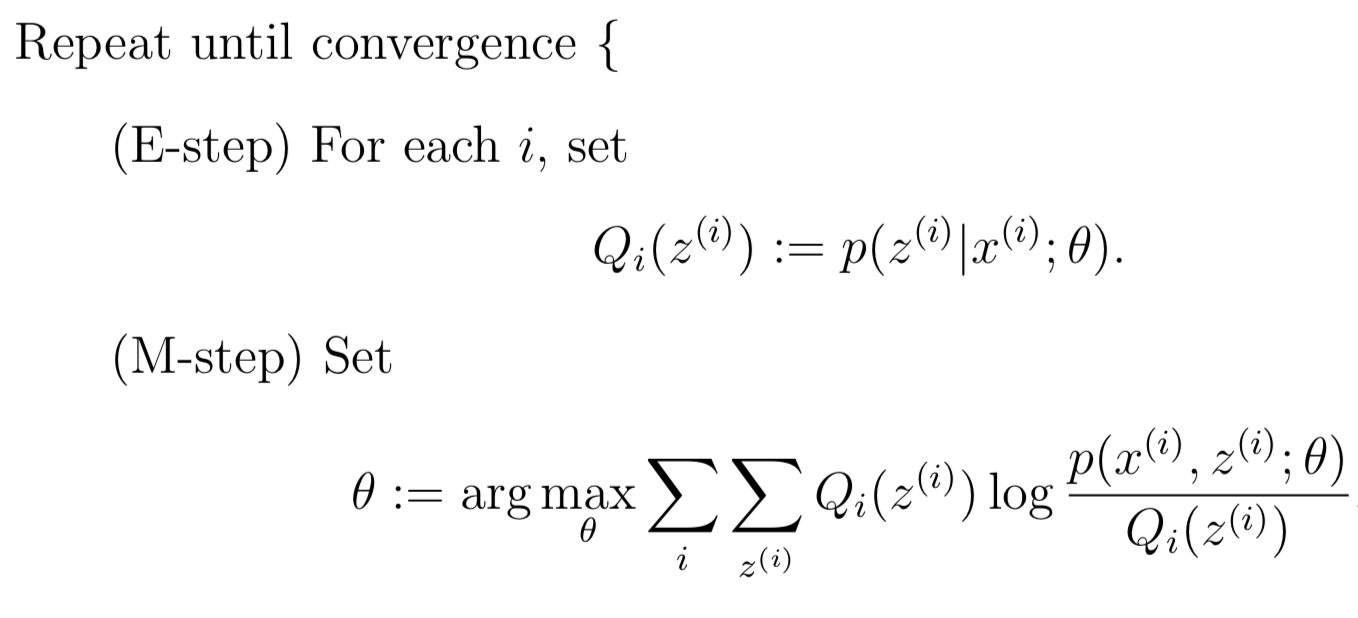
之前我们根据图像,形象的理解了EM算法选取下界函数并收敛。但是如何理论证明EM一定收敛呢,那就要证明θ(t)处得到下界函数后,maximize下界函数得到新的参数θ(t+1),那么一定满足l(θ(t)) ≤ l(θ(t+1))。接下来就来证明这一点
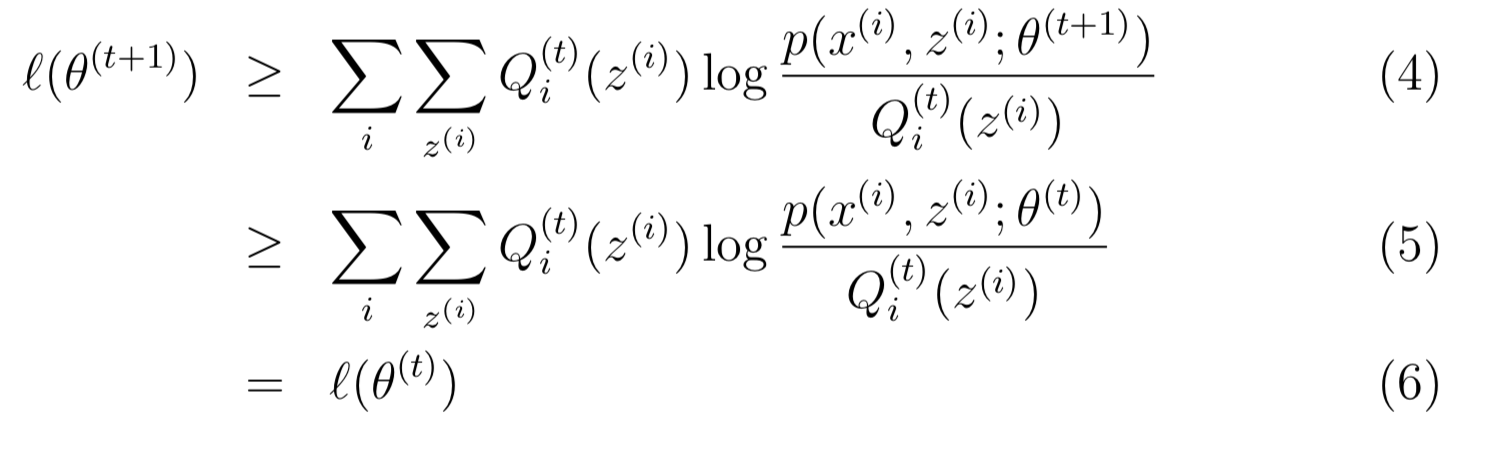
上述公式(4)(5)(6)如何来的呢,首先解释第一个,因为Jensen不等式可以知道
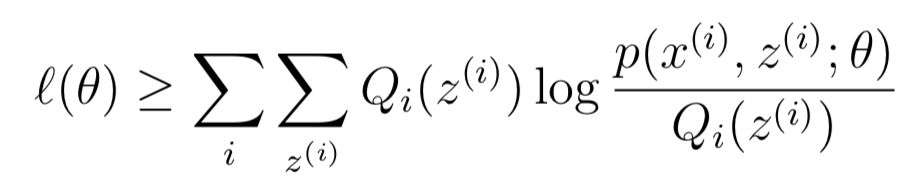
对于任意的分布Qi和θ都成立,那么对于Qi = Qi(t), θ = θ(t+1)也一定成立。对于公式(5),θ(t+1)是通过最大化来的:
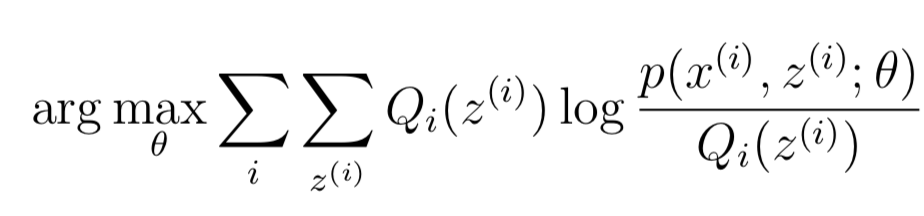
因此,从(4)到(5)很好理解。至此,证明了EM算法一定会收敛。
其实如果我们做如下定义:
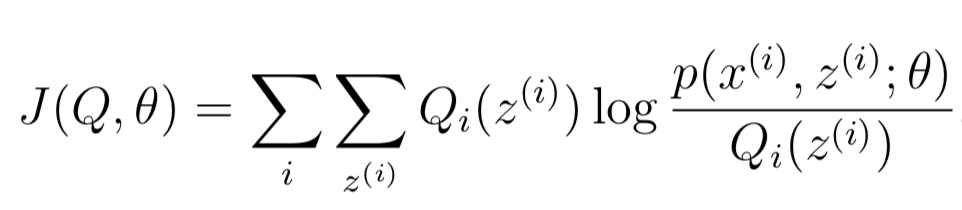
同时存在l(θ) ≥ J(Q,θ),因此EM算法可以看成是关于Q和θ的坐标上升算法。E-step关于Q对J做最大化,M-step关于θ对J做最大化。
3-2. 混合高斯回顾(基于EM)
根据EM算法,E-Step 计算:
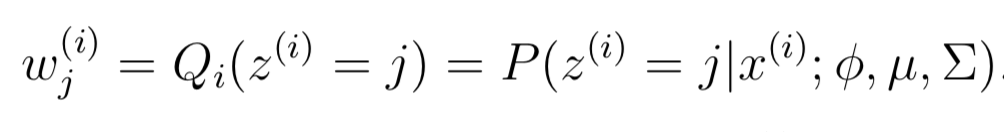
接下来 M-Step 针对参数φ, μ, Σ 进行maximize:
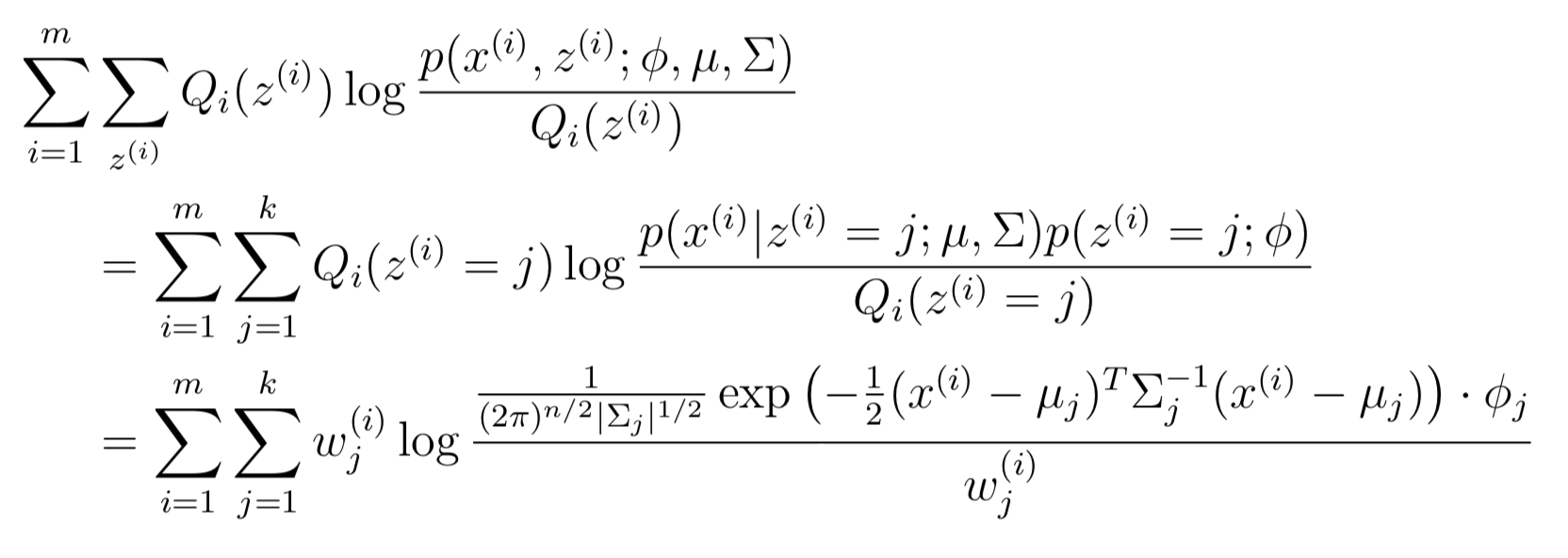
首先基于μl进行maximize,并求导数:
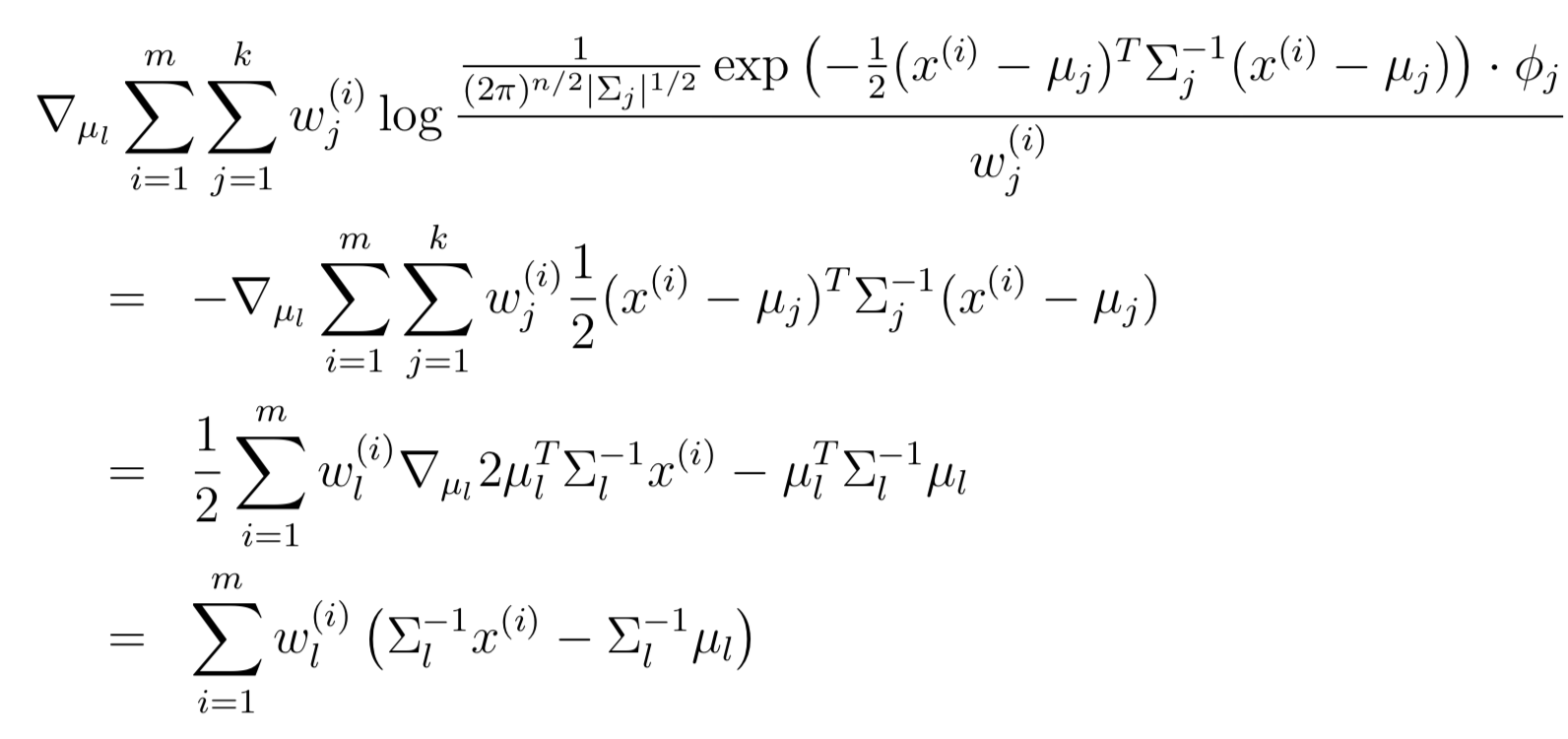
导数设为0,求解μl的更新规则:
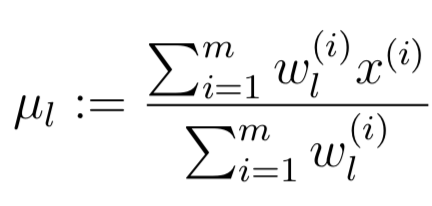
下面分析参数φj,其实与φj有关的很少,只需要最大化:
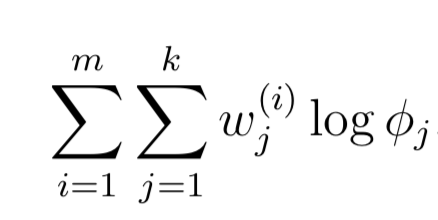
因为是概率分布,因此Sum(φj)=1,因此采用拉格朗日Lagrangian:
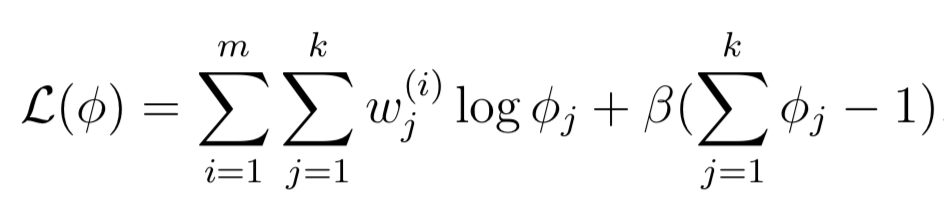
求导数等于0,就可以求的φj:
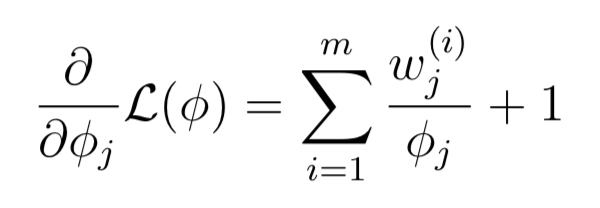
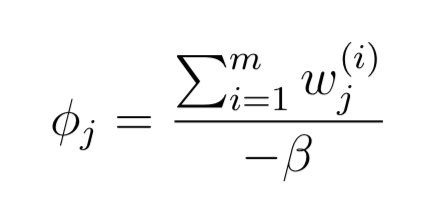
因为Sum(φj)=1,而且φj与Sum(w)成正比,同时wj=Qi(z(i) = j)因此:
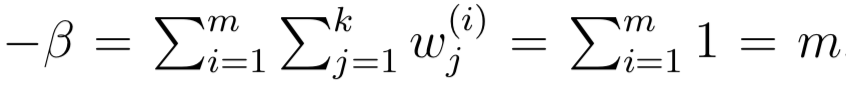
从而φj的更新公式如下: