激活函数-性质
- 非线性:即导数不是常数。保证多层网络不退化成单层线性网络。这也是激活函数的意义所在。
- 可微性:保证了在优化中梯度的可计算性。虽然ReLU存在有限个点处不可微,但处处subgradient,可以替代梯度
- 计算简单:激活函数复杂就会降低计算速度,因此RELU要比Exp等操作的激活函数更受欢迎。
- 非饱和性(saturation):饱和指的是在某些区间梯度接近于零(即梯度消失),使得参数无法继续更新的问题。最经典的例子是Sigmoid,它的导数在x为比较大的正值和比较小的负值时都会接近于0。RELU对于x<0,其梯度恒为0,这时候它也会出现饱和的现象。Leaky ReLU和PReLU的提出正是为了解决这一问题。
- 单调性(monotonic):即导数符号不变。当激活函数是单调的时候,单层网络能够保证是凸函数。但是激活函数如mish等并不满足单调的条件,因此单调性并不是硬性条件,因为神经网络本来就是非凸的
- 参数少:大部分激活函数都是没有参数的。像PReLU带单个参数会略微增加网络的大小。还有一个例外是Maxout,尽管本身没有参数,但在同样输出通道数下k路Maxout需要的输入通道数是其它函数的k倍,这意味着神经元数目也需要变为k倍;但如果不考虑维持输出通道数的情况下,该激活函数又能将参数个数减少为原来的k倍。
激活函数-简介
一、sigmoid激活函数
sigmoid函数及其导数如下:

优点
- 梯度平滑
- 输出值在0-1之间
缺点
- 激活函数计算量大(在正向传播和反向传播中都包含幂运算和除法)
- 梯度消失:输入值较大或较小(图像两侧)时,sigmoid函数值接近于零。sigmoid导数则接近于零,导致最终的梯度接近于零,无法实现更新参数的目的。
- Sigmoid的输出不是0为中心(zero-centered)
二、tanh激活函数
tanh函数及其导数:
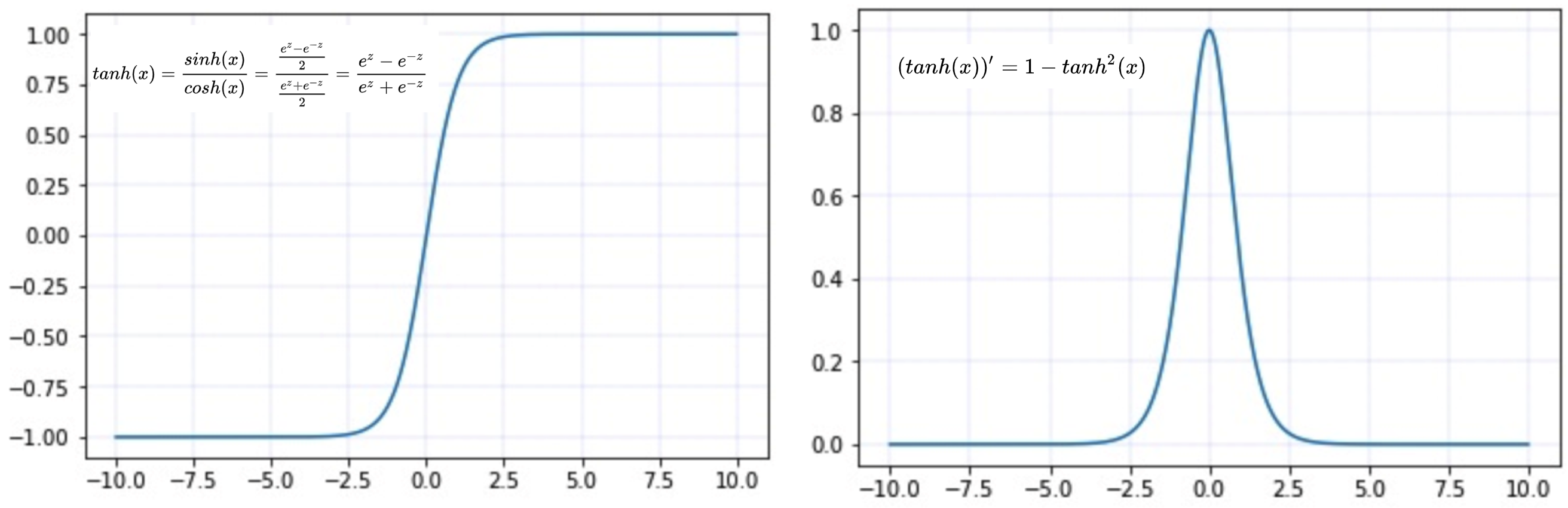
优点
- 同sigmoid
- tanh(x)的梯度消失问题比sigmoid要轻,收敛更快
- 输出是以0为中心 zero-centered
缺点
- 同 sigmoid
三、整流线性单元(ReLU)
relu的函数及其导数如下

优点
- 简单高效:不涉及指数等运算
- 一定程度缓解梯度消失问题:因为导数为1,不会向sigmoid那样由于导数较小,而导致连乘得到的梯度逐渐消失。
缺点
- dying Relu:即网络的部分分量都永远不会更新,可以参考what-is-the-dying-relu-problem-in-neural-networks
四、指数线性单元(ELU)
elu的函数及其导数如下

优点
- 能避免死亡 ReLU 问题:x小于0时函数值不再是0,因此可以避免dying relu问题。
- 能得到负值输出,这能帮助网络向正确的方向推动权重和偏置变化;
缺点
- 计算耗时:包含指数运算;
- α 值是超参数,需要人工设定
五、扩展型指数线性单元激活函数(SELU)
selu源于论文Self-Normalizing Neural Networks作者为 Sepp Hochreiter,ELU 同样来自于他们组。 selu其实就是ELU乘lambda,关键在于这个lambda是大于1的,论文中给出了lambda和alpha的值
- lambda = 1.0507
- alpha = 1.67326
selu的函数及其导数如下

优点
- SELU 激活能够对神经网络进行自归一化(self-normalizing);
- 不可能出现梯度消失或爆炸问题,论文附录的定理 2 和 3提供了证明
缺点
- 应用较少,需要更多验证。
- lecun_normal和Alpha Dropout:需要 lecun_normal 进行权重初始化;如果 dropout,则必须用 Alpha Dropout 的特殊版本
六、渗漏型整流线性单元激活函数(Leaky ReLU)
leak_relu的函数及其导数如下

优点
- 类似于ELU,能避免死亡 ReLU 问题:x小于0时候,导数是一个小的数值,而不是0。
- 于ELU类似,能得到负值输出
- 计算快速:不包含指数运算
缺点
- 同ELU,α 值是超参数,需要人工设定
- 在微分时,两部分都是线性的;而 ELU 的一部分是线性的,一部分是非线性的
七、Parametric ReLU(PRELU)

形式上与Leak_ReLU在形式上类似,不同之处在于:PReLU的参数alpha是可学习的,需要根据梯度更新。
- alpha=0:退化为ReLU
- alpha固定不更新,退化为Leak_ReLU
优点
- 与ReLU相同
缺点
- 在不同问题中,表现不一
八、高斯误差线性单元(Gaussian Error Linear Unit,GELU)
Dropout和ReLU都希望将“不重要”的激活信息变为零。以ReLU为例,对于每个输入x都会乘以一个分布,这个分布在x>0时为常数1,在x<=0时为常数0。而GELU也是在x(服从标准正态分布)的基础上乘以一个分布,这个分布就是伯努利分布Φ(x) = P(X ≤ x)。
因此,高斯误差线性单元(GELU)为 GELU(x) = x*P(X ≤ x)
- 随着 x 的降低,它被归零的概率会升高。对于 ReLU 来说,这个界限就是 0,输入少于零就会被归零。
- 与RELU类似:对输入的依赖;
- 与RELU不同:软依赖P(X ≤ x),而非简单0-1依赖
- 直观理解:可以按当前输入 x 在其它所有输入中的位置来缩放 x
但是这个函数无法直接计算,需要通过另外的方法来逼近这样的激活函数,研究者得出来两个逼近函数:

第二个逼近函数,与谷歌 2017 年提出来的 Swish 激活函数类似:f(x) = x · sigmoid(x),后面详细介绍
以第一个近似函数为例,GELU的函数及其导数如下

优点
- 在 NLP 领域效果最佳;尤其在 Transformer 模型中表现最好;
- 类似RELU能避免梯度消失问题。
缺点
- 2016年提出 较新颖
- 计算量大:类似ELU,涉及到指数运算
九、Swish by google 2017
Swish激活函数形式为: f(x) = x * sigmoid(βx)
- β是个常数或可训练的参数,通常所说的Swish是指β=1
- β=1.702时,可以看作是GELU激活函数

优点
- 据论文介绍,Swish效果由于ReLU
缺点
- 计算量大:sigmoid涉及到指数运算
十、Mish by Diganta Misra 2019
Mish=x * tanh(ln(1+e^x))
在函数形式和图像上,都与GELU和Swish(β=1)类似

优点
根据论文介绍:
- Mish函数保证在曲线上几乎所有点上的平滑度
- 随着层深的增加,ReLU精度迅速下降,其次是Swish。而Mish能更好地保持准确性。
缺点
- 2019年提出,需要时间和更多实际应用验证
十一、Maxout
maxout的参数量较大,因此实际应用中比较少

普通网络每一层只有一个参数矩阵W,maxout则有k个参数W,每个隐藏单元只取k个W*x+b的计算结果中最大的。下图比较形象:

- maxout可以拟合任意的的凸函数
- Maxout与Dropout的结合效果比较好